Mathematical Definition: Momentum is the product of an object's mass and its velocity. The equation is given as p = mv, where p represents momentum, m is mass, and v is velocity. Momentum is a vector quantity as it has a direction.
Units of Momentum: The unit of momentum is kg m s⁻¹, and it does not have a special name in the SI system.
Principle of Conservation of Momentum: In a closed system, the total momentum of all objects before an interaction is equal to the total momentum of all objects after the interaction. A closed system is one in which there are no external forces acting.
The principle of conservation of momentum (PCM) is used to model collisions. The basic equation of PCM is: $$m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2$$
A collision is an event where two objects collide and cause their velocities to change.

Springy and Sticky Collisions

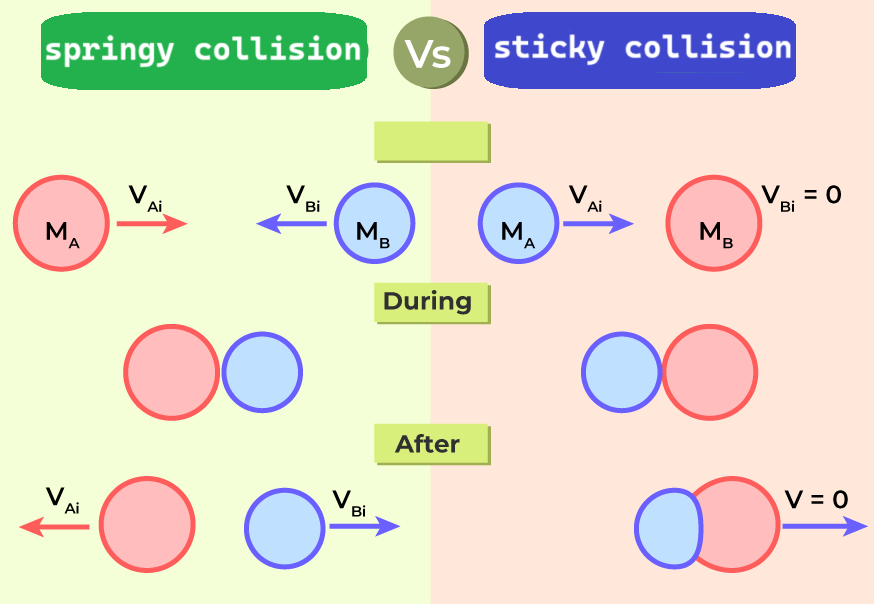
Collisions: When two objects collide, they interact with each other, and momentum is transferred between them. However, the total momentum of the two objects remains the same before and after the collision.
A sticky collision is where two objects "stick together" after a collision.
A springy collision is where two objects are separated after the collision.
All sticky collisions are inelastic.
Most springy collisions are elastic but some may be inelastic.

Modelling 1D Collision Example

Total k.e. must remain the same.
Total momentum must also remain the same.
$$\begin{align*} m_1u_1 + m_2u_2 &= m_1v_1 + m_2v_2 \\ 2(4) + 3(0) &= 2v_1 + 3v_2 \\ 2v_1 + 3v_2 &= 8 \quad\text{(1)} \\ \frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 &= \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 \\ \frac{1}{2}(2)(4)^2 + \frac{1}{2}(3)(0)^2 &= \frac{1}{2}(2)v_1^2 + \frac{1}{2}(3)v_2^2 \\ v_1^2 + \frac{3}{2}v_2^2 &= 16 \quad\text{(2)} \\ v_1 &= \frac{8-3v_2}{2} \quad\text{(3)} \\ \text{Sub (3) into (2)} \\ \left(\frac{8-3v_2}{2}\right)^2 + \frac{3}{2}v_2^2 &= 16 \\ \frac{64 - 48v_2 + 9v_2^2}{4} + \frac{3}{2}v_2^2 &= 16 \\ 16 - 12v_2 + \frac{9}{4}v_2^2 + \frac{3}{2}v_2^2 &= 16 \\ \frac{15}{4}v_2^2 - 12v_2 &= 0 \\ v_2 &= 3.2, 0 \quad\text{(0 is rejected)} \\ v_1 &= \frac{8-3(3.2)}{2} = -0.8 \\ \text{Thus, } v_1 &= -0.8 \, \text{ms}^{-1} \text{ and } v_2 = 3.2 \, \text{ms}^{-1}\end{align*}$$

In elastic collisions, kinetic energy (k.e.) is conserved. The relative speed of approach is equal to the relative speed of separation. The total k.e. before and after the collision remain the same.
In inelastic collisions, kinetic energy is not conserved. Some k.e. is converted into other forms of energy. The total k.e. before and after the collision is different.

Newton's First Law (Law of Inertia): An object will remain at rest or keep traveling at a constant velocity unless it is acted upon by a resultant force. Thus, an object's momentum will not change unless there is a resultant force acting on it.
Newton's Second Law: The resultant force acting on an object is equal to the rate of change of its momentum. It can be expressed as: $$F = \frac{mv - mu}{t} \\ = \frac{m(v - u)}{t} \\= m \left( \frac{v - u}{t} \right) \\= ma$$
Newton's Third Law: When two bodies interact, the forces they exert on each other are equal and opposite. During a collision, the change in momentum of one object is equal and opposite to the change in momentum of the other object.
For example, if the momentum of one ball decreases by 2kgms-1, the momentum of the other ball will increase by 2kgms-1.