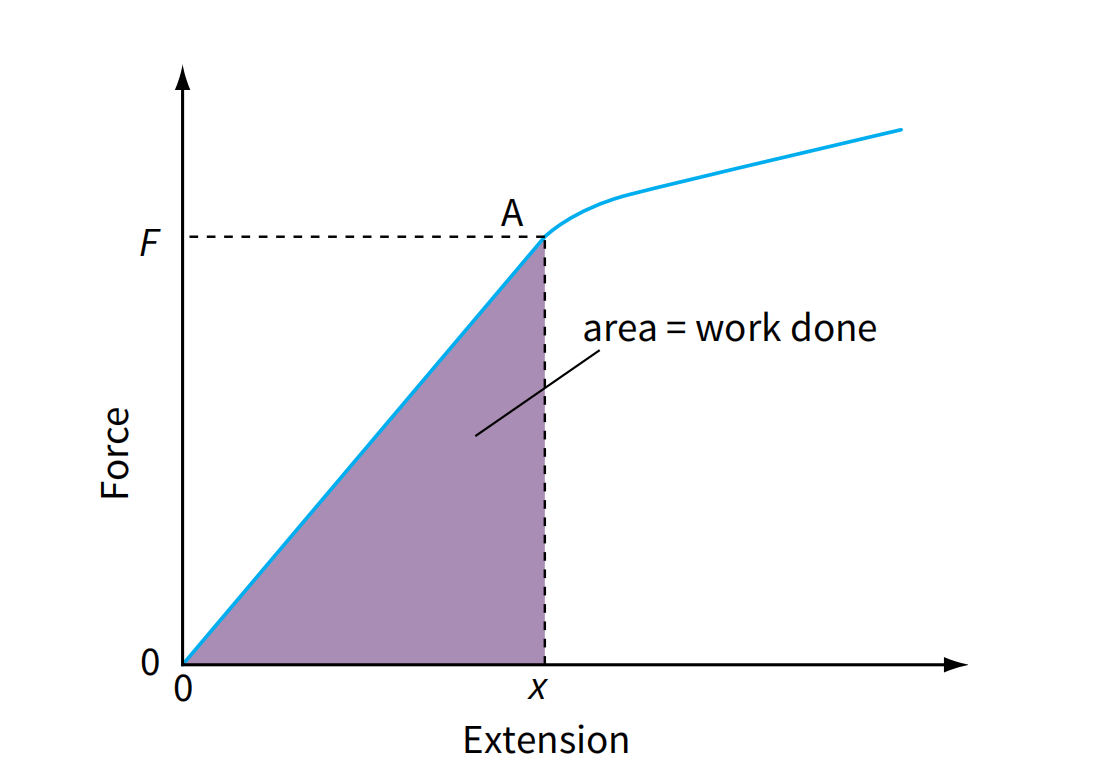
Understanding a force-extension graph

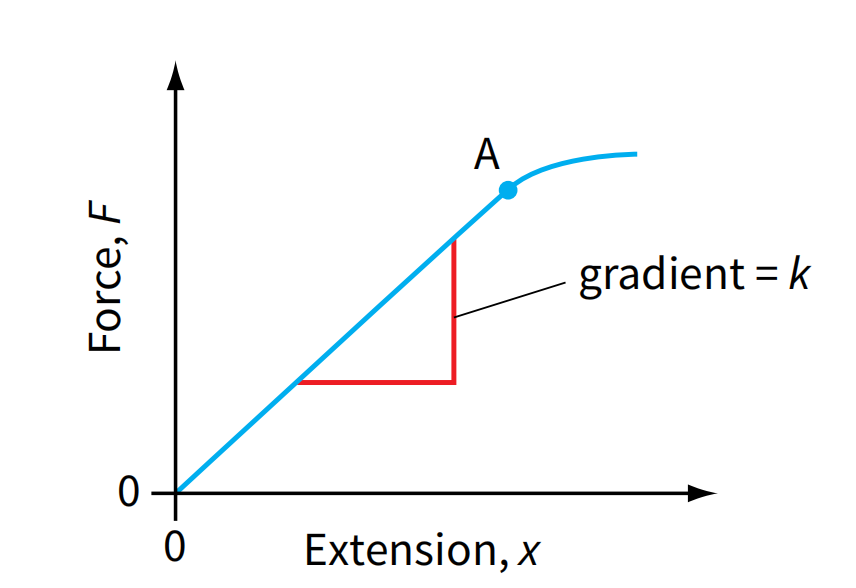
The graph typically has force (F) on the y-axis. This is usually measured in newtons (N).
The extension (x) is on the x-axis. This is measured in units of length). Note that the extension is the increase in length of the material, not its total length.
The linear region (origin to A), represents the material obeying Hooke's Law, where F=kx.
The gradient of this straight-line portion represents the spring constant (k). A steeper gradient indicates a stiffer material, which requires a greater force to produce the same extension.
After the elastic limit (A), the force-extension graph curves, meaning that the extension is no longer proportional to the applied force.
If the elastic limit is breached, the material no longer returns to its original length when the force is removed. (permanent deformation)

F-E graphs and work done

The area under the force-extension graph represents the work done in stretching or compressing the material. This work done is equal to the elastic potential energy stored in the material.
When a material obeys Hooke's law, the elastic potential energy (E) can be calculated using: \( E = \frac{1}{2} Fx \) or \( E = \frac{1}{2} kx^2 \).
If the graph is not a straight line, the area under the graph must be determined by counting squares or using other methods to estimate the area.
If the material has been plastically deformed (beyond the elastic limit), some of the work done is converted into thermal energy, and the energy cannot be fully recovered when the material is released.