If the object moves in the exact same direction of the force, we can simply use the equation W=Fs. For example, if we are pushing a box horizontally along the floor with 30N of force for 5m, the calculations will be as simple as: W = Fs = 30 x 5 = 150J
If the force and movement are in different directions, then you need to use the component of the force that’s going in the direction of movement, so you have to use W = Fs cos θ.
When an object falls from a height, gravity can be considered to be "doing work" on the object. $$\begin{align*} W &= Fs \\ F &= \text{force of gravity on object} = mg \\ S &= \text{distance moved} = \text{height}, h \\ W &= (mg)h \\ &= mgh \end{align*}$$
If force is acting on an object, but the object isn't moving in the direction of the force, then the work done is 0. $$\begin{align*}s &= \text{distance moved} = 0 \\ W &= Fs \\&= F \times 0 \\&=0\end{align*}$$

GPE and KE

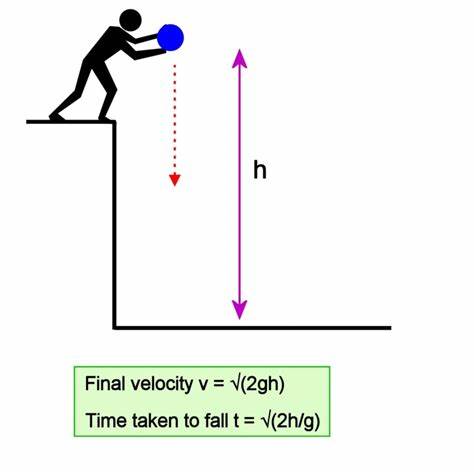
Energy is often converted from one type to another. Once common example is gravitational potential energy (gpe) to kinetic energy (ke) and vice versa.
We calculate KE using: KE = 1/2 mv² where m = mass and v = speed
We calculate GPE using: GPE = mgh , where m = mass, g = gravity and h = height
When an object is falling from a height, GPE is converted to KE. We can use this to calculate the velocity of an object right before it hits the ground.
$$\begin{align*}mgh &= \frac{1}{2} mv^2 \\2gh &= v^2 \\v &= \sqrt{2gh}\end{align*}$$

Calculating Work Done Example

The motion isn't exactly in direction of the force, so we must find the component of the force in the direction of motion.
$$\begin{align*} F_x &= F \cos \theta \\&= F \cos 30^\circ \\&= 100 \cos 30^\circ \\&= 15.43 \, \text{N} \\\\W &= Fs \\&= 15.43 \times 15 \\&= 231.45\, \text{J}\end{align*}$$

Power is the rate at which work is done. In other words, how fast is energy being transferred.
We calculate it using the formula $P &= \frac{W}{t}$ where P is power, W is work done, and t is time taken.
Power can also be calculated by the formula P = F × v which is the force multiplied by the speed. This applies to situations such as cars or aircraft.