What are Kirchoff's Laws?

Kirchhoff's laws are fundamental principles used to determine current and p.d. at specific parts of complicated circuits. 

Kirchoff's First Law

  • The total current entering any point in a circuit must equal to the total current leaving that same point.
  • This is a consequence of the conservation of charge, meaning that the amount of charge entering a point must be the same as the amount of charge exiting.
  • For example, if a 5.0 A current enters a junction and splits into two branches, the sum of the currents in the two branches must be 5.0 A.
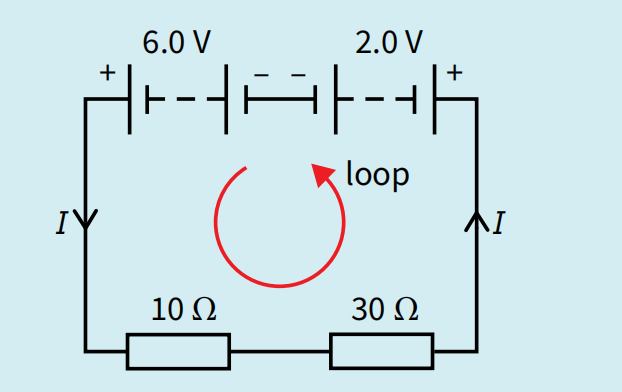
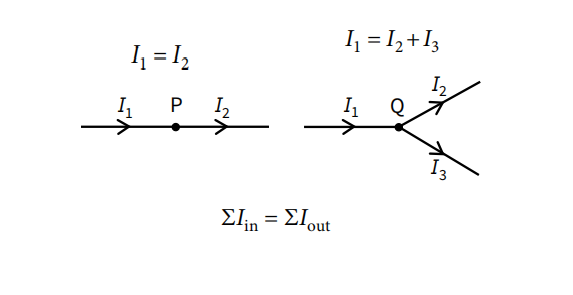Mobirise Website Builder

Kirchoff's Second Law

  • The sum of the electromotive forces (e.m.f.s) around any closed loop in a circuit is equal to the sum of the potential differences (p.d.s) around the same loop.
  • This law is a consequence of the conservation of energy.
  • If a charge moves around a loop, it gains energy from e.m.f. sources and loses energy across components with p.d.s, and the total energy gained must equal the total energy lost.
Mobirise Website Builder

Using Kirchoff's Laws to solve problems



$$\begin{align*}I_1 + I_2 &= I_3 \quad \text{(Equation 1)}\\\text{Loop 1:}\\\text{Sum of p.d} &= \text{Sum of emf}\\I_3(50) + I_1(10) &= 6\\10I_1 + 30I_3 &= 6 \quad \text{(Equation 2)}\\\text{Loop 2:}\\\text{Sum of p.d} &= \text{Sum of emf}\\I_3(30) &= 2\\I_3 &= \frac{2}{30} = 0.0667 \, \text{A}\\\text{Substitute } I_3 \text{ into Equation 2:}\\10I_1 + 30(0.0667) &= 6\\10I_1 + 2.00 &= 6\\10I_1 &= 4.00\\I_1 &= \frac{4}{10} = 0.4 A\\\text{From Equation 1:}\\I_2 &= I_3 - I_1\\I_2 &= 0.0667 - 0.400\\I_2 &= -0.333 A\\\text{Thus, } I_1 &= 0.4 \, \text{A}, \quad I_2 = -0.333 \, \text{A}, \quad I_3 = 0.0667 \, \text{A} \end{align*}$$

Download PDF

© Copyright 2025 Lecturemate - All Rights Reserved