Vectors for a rectangle shape

$ \overrightarrow{OA} $ and $ \overrightarrow{OC} $ are always parallel.
$ \overrightarrow{DA} $ is always perpendicular to $ \overrightarrow{AB} $, $ \overrightarrow{AB} $ is always perpendicular to $ \overrightarrow{BC} $, $ \overrightarrow{BC} $ is perpendicular to $ \overrightarrow{CD} $ and $ \overrightarrow{CD} $ is perpendicular to $ \overrightarrow{DA} $.
$ \overrightarrow{OA} \cdot \overrightarrow{AB} $, $ \overrightarrow{AB} \cdot \overrightarrow{BC} $, $ \overrightarrow{BC} \cdot \overrightarrow{CD} $, $ \overrightarrow{CD} \cdot \overrightarrow{DA} $ all equal to 0.
Diagonals intersect at $ \frac{1}{2} \overrightarrow{OB} $ or $ \frac{1}{2} \overrightarrow{AD} $.
$ |\overrightarrow{OA}| = |\overrightarrow{OC}| $
$ |\overrightarrow{AB}| = |\overrightarrow{CD}| $

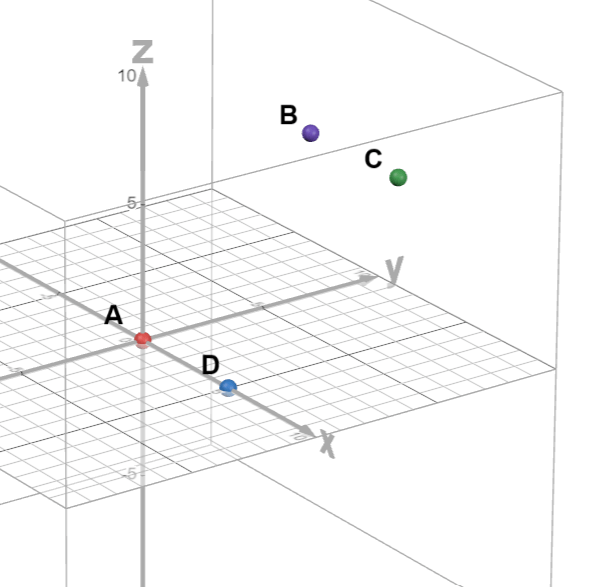
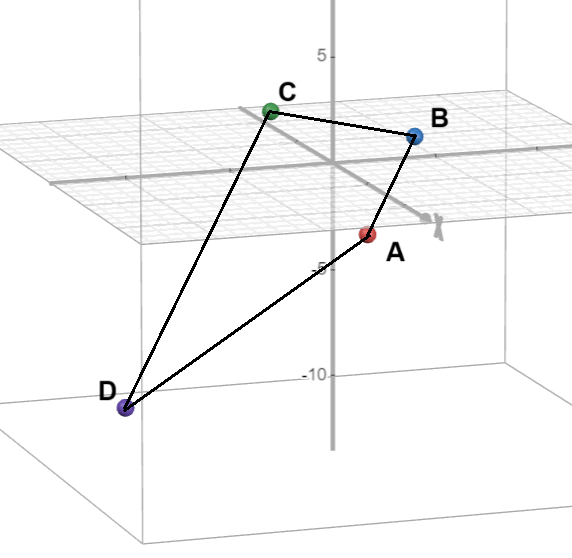
Finding intersection of diagonals

$ \overrightarrow{OA} = \begin{pmatrix} 2\\ 1 \\ -3 \end{pmatrix} $, $ \overrightarrow{OB} = \begin{pmatrix} 0 \\ 4 \\ 1 \end{pmatrix} $, $ \overrightarrow{OC} = \begin{pmatrix} -3 \\ -2 \\ 1 \end{pmatrix} $, $ \overrightarrow{OD} = \begin{pmatrix} 3 \\ -11 \\ -10 \end{pmatrix} $

$ \overrightarrow{AC} = \overrightarrow{AO} + \overrightarrow{OC} = \begin{pmatrix} -2\\ -1 \\ 3 \end{pmatrix} + \begin{pmatrix} -3\\ -2 \\ 2 \end{pmatrix} = \begin{pmatrix} -5\\ -3 \\ 5 \end{pmatrix}$

$ \overrightarrow{BD} = \overrightarrow{BO} + \overrightarrow{OD} = \begin{pmatrix} 0\\ -4 \\ -1 \end{pmatrix} + \begin{pmatrix} 3\\ -11 \\ -10 \end{pmatrix} = \begin{pmatrix} 3\\ -15 \\ -11 \end{pmatrix}$

line $ \overrightarrow{AC} = \begin{pmatrix} 2\\ 1 \\-3 \end{pmatrix} + x \begin{pmatrix} -5\\ -3 \\ 5\end{pmatrix} $

line $ \overrightarrow{BD} = \begin{pmatrix} 0 \\4 \\ 1 \end{pmatrix} + y \begin{pmatrix} -3 \\ -15 \\ -11 \end{pmatrix} $

$$\begin{pmatrix} 0 \\ 4 \\ 7 \end{pmatrix} + y \begin{pmatrix} 3 \\ -15 \\ -1 \end{pmatrix} = \begin{pmatrix} 3 \\ -15 \\ -11 \end{pmatrix}$$

$$\begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix} + x \begin{pmatrix} -3 \\ -5 \\ 1 \{
\end{pmatrix} = \begin{pmatrix} 0 \\ 4 \\ 7 \end{pmatrix} + y \begin{pmatrix} 3 \\ -15 \\ -11 \end{pmatrix}$$

$$\begin{pmatrix} 2 - 3x \\ 1 - 5x \\ -3 + x \end{pmatrix} = \begin{pmatrix} 3y \\ 4 - 15y \\ 7 - 11y \end{pmatrix}$$

2 - 3x = 3y
1 - 5x = 4 - 15y

Equation 1: 3x + 3y = 2
Equation 2: 5x - 15y = -3

Solving the simultaneous linear equations we get:
$ x = \frac{1}{4}, y = \frac{2}{3} $

Position vector of diagonal intersection = $ \begin{pmatrix} 2 - 3(\frac{1}{4}) \\ 1 - 5(\frac{1}{4}) \\ -3 + (\frac{1}{4}) \end{pmatrix} = \begin{pmatrix} \frac{5}{4} \\ -\frac{1}{4} \\ -\frac{11}{4} \end{pmatrix} $

Finding the angles between diagonals
[This is unrelated to finding the intersection between diagonals. However, I added this here as it is a rather important part of the syllabus]

$ \vec{AC} \cdot \vec{BD} = \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 4 \\ 1 \end{pmatrix} = 2(0) + 1(4) + (-3)(1) = 2 $

$ |\vec{AC}| = \sqrt{2^2 + 1^2 + (-3)^2} = \sqrt{14} $

$ |\vec{BD}| = \sqrt{0^2 + 4^2 + 1^2} = \sqrt{17} $

$ \vec{AC} \cdot \vec{BD} = |\vec{AC}| |\vec{BD}| \cos \theta $

$ 2 = \sqrt{14} \sqrt{17} \cos \theta $

$ \theta = \cos^{-1} \left( \frac{2}{\sqrt{14} \sqrt{17}} \right) = 82.6^\circ $

Vectors for a rectangle shape

Vectors for a trapezium

Finding intersection of diagonals