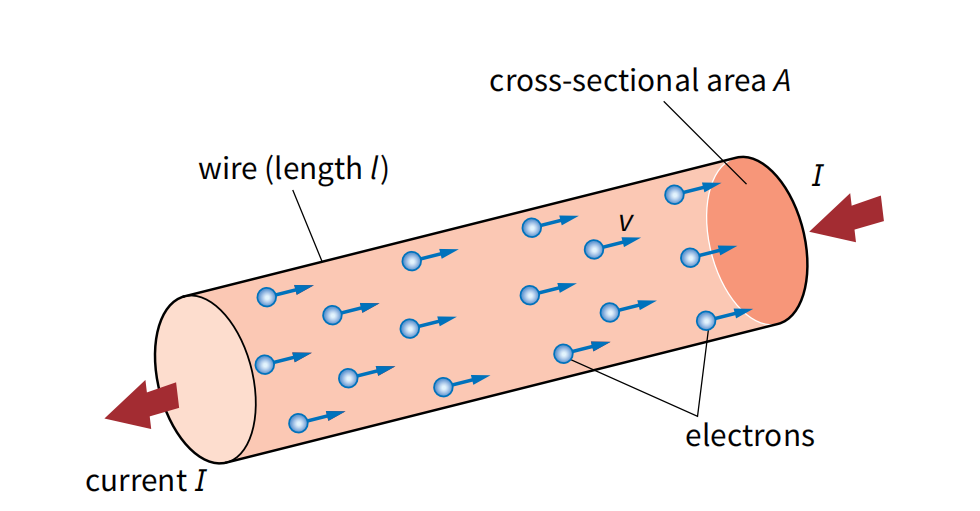
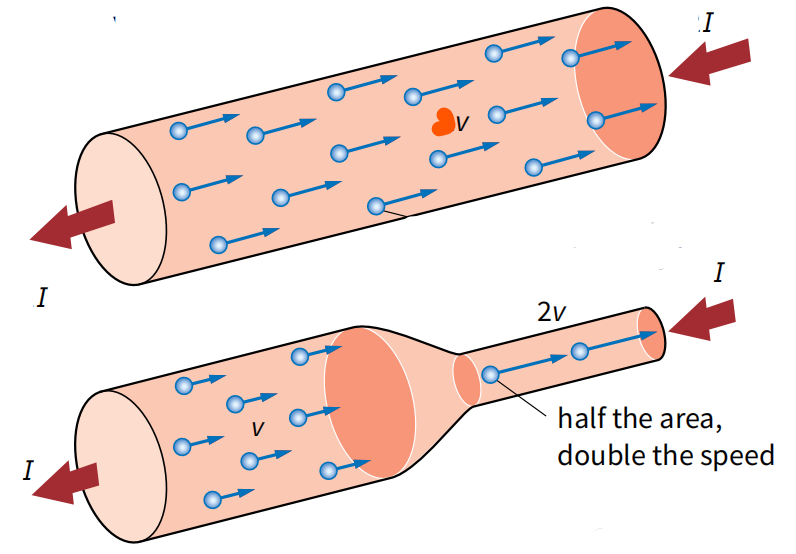
Breaking down the equation
- n is the number density of charge carriers, which is the number of charge carriers per unit volume of the material, typically measured in m⁻³.
- A is the cross-sectional area of the conductor, measured in square meters (m²).
- q represents the charge of each charge carrier, measured in coulombs (C). For electrons, this is the elementary charge e, where e = 1.6 × 10⁻¹⁹ C.
- v is the average drift velocity of the charge carriers, measured in meters per second (m s⁻¹).
- Note: Average drift velocity is merely the speed at which one charge carrier moves from one end of the conductor to the other, given by the equation \( l/t \). The actual speed is a lot higher but the charge carriers bounce around as they move through the conductor, making their path longer.