2D Collisions

When modelling 2D collisions, momentum must be conserved in both the x and y components.

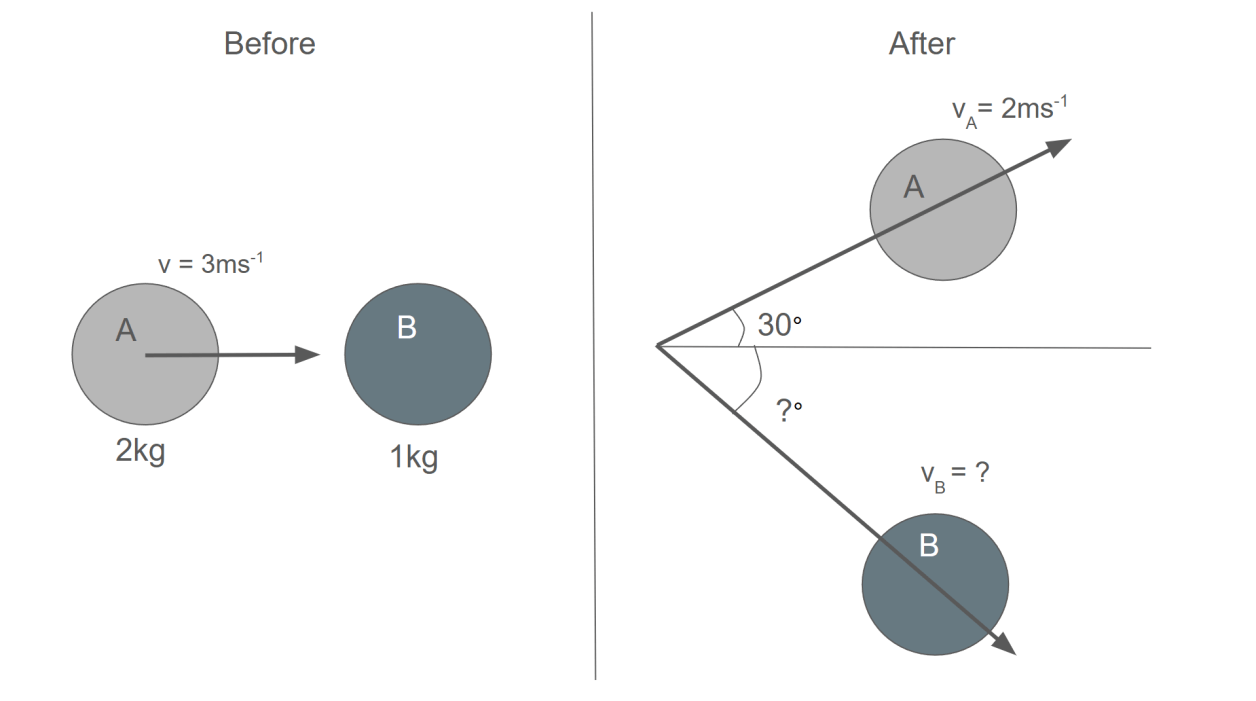
Steps In Modelling 2D Collisions

  1. Begin by breaking down the velocities of all objects involved in the collision into their x and y components. If a velocity v is at an angle θ to the x-axis, the x-component is vcos(θ), and the y-component is vsin(θ).
  2. The principle of conservation of momentum is applied separately in the x-direction and the y-direction. 
  3. Using the equations set up in the previous step, solve for the unknown quantities. They can be v, θ, or m depending on the question.
Mobirise Website Builder

2D Collision Question Example

  1. Question: Find the velocity and angle of ball B after the collision.
  2. Initial x-momentum: \( (2 \text{ kg} \cdot 3 \text{ m/s}) + (1 \text{ kg} \cdot 0) = 6 \text{ kg m/s} \).
    Initial y-momentum: 0

    Final x-momentum of ball Al: \( 2 \text{ kg} \times 2 \text{ m/s} \times \cos(30^\circ) = 3.46 \text{ kg m/s} \).
    Final y-momentum of ball A: \( 2 \text{ kg} \times 2 \text{ m/s} \times \sin(30^\circ) = 2 \text{ kg m/s} \).

    X-direction: \( 6 = 3.46 + (1 \text{ kg} \times v_{bx}) \). Therefore, \( v_{bx} = 2.54 \text{ m/s} \).
    Y-direction: \( 0 = 1 + (1 \text{ kg} \times v_{By}) \). Therefore, \( v_{By} = -1 \text{ m/s} \).

    The magnitude of the velocity of ball B: \( \sqrt{2.54^2 + (-1)^2} = 2.73 \) m/s.
    The direction of the velocity of the 1 kg ball: \( \tan^{-1}(-1/2.54) = -21.5^\circ \) relative to the x-axis.

Mobirise Website Builder
Download PDF

© Copyright 2025 Lecturemate - All Rights Reserved