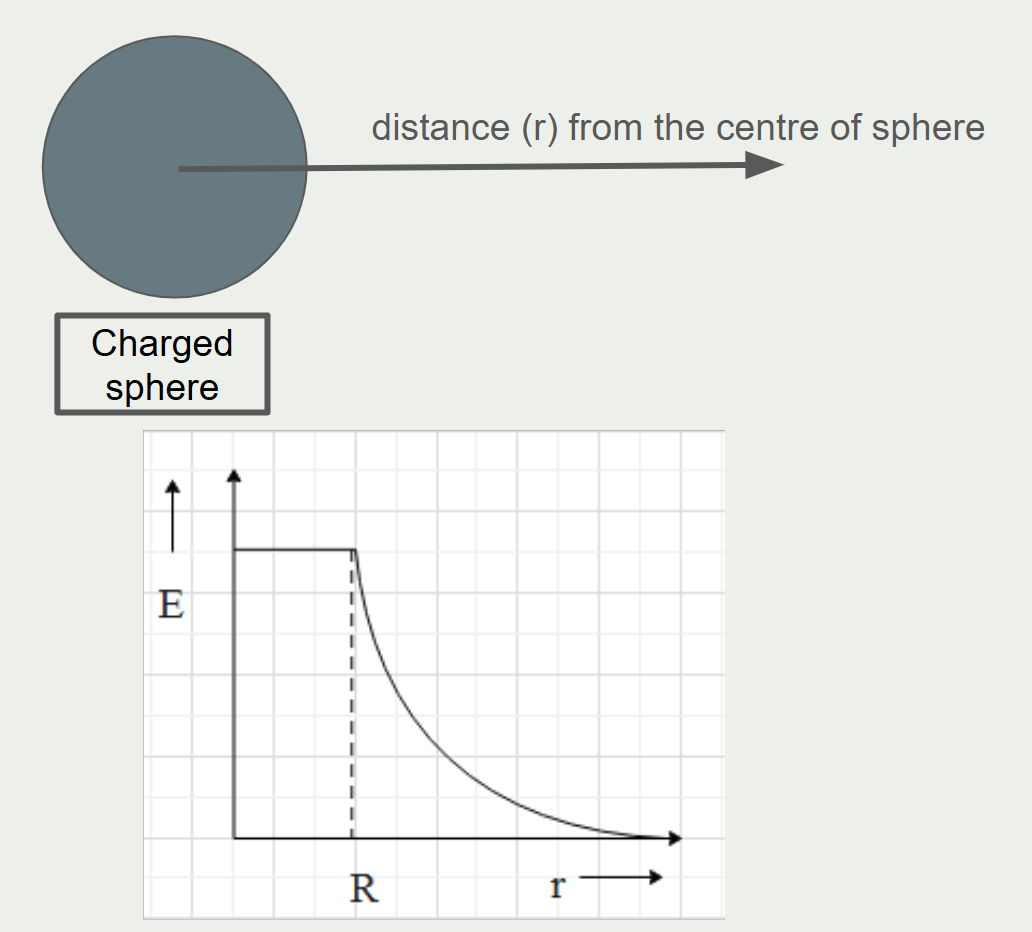
Electric potential graph for one sphere
- The electric potential of a sphere is given by the equation \(E = \frac{Q}{4 \pi \varepsilon_0 r}\).
- Q represents the total charge on the sphere surface.
- \(𝜀_{0}\) is a constant that represents the permittivity of air.
- E is constant inside the sphere as the charges are evenly spaced out on the surface of the sphere.
- E decreases as r increases outside the sphere because \(𝜀_{0}\) and Q remain the same. Thus, \( E \propto \frac{1}{r} \)
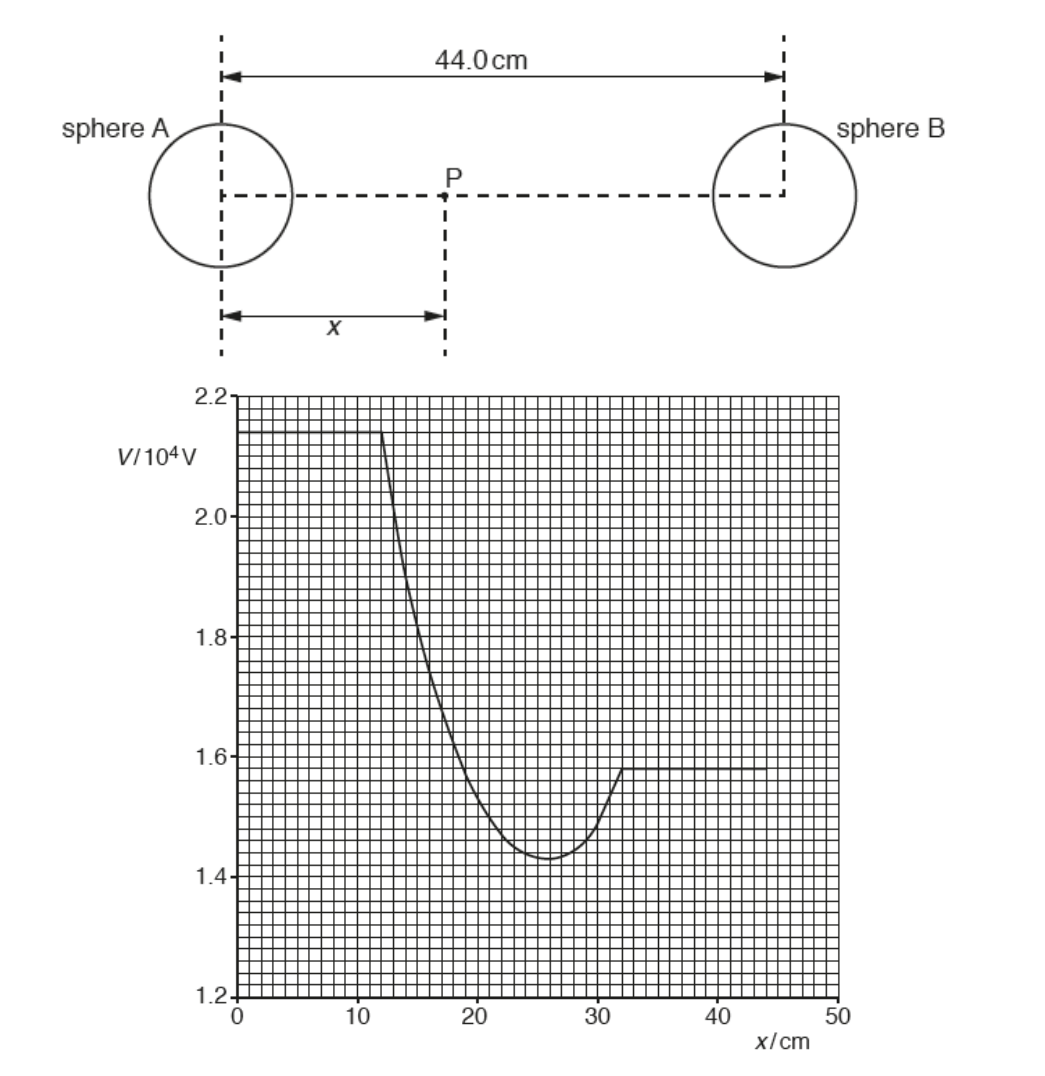
- For two spheres, the electric potential at a particular point is the sum of the potentials of both spheres. In this case, it would be given by: $$E = \frac{Q_{A}}{4 \pi \varepsilon_0 r} + \frac{Q_{B}}{4 \pi \varepsilon_0 r}$$