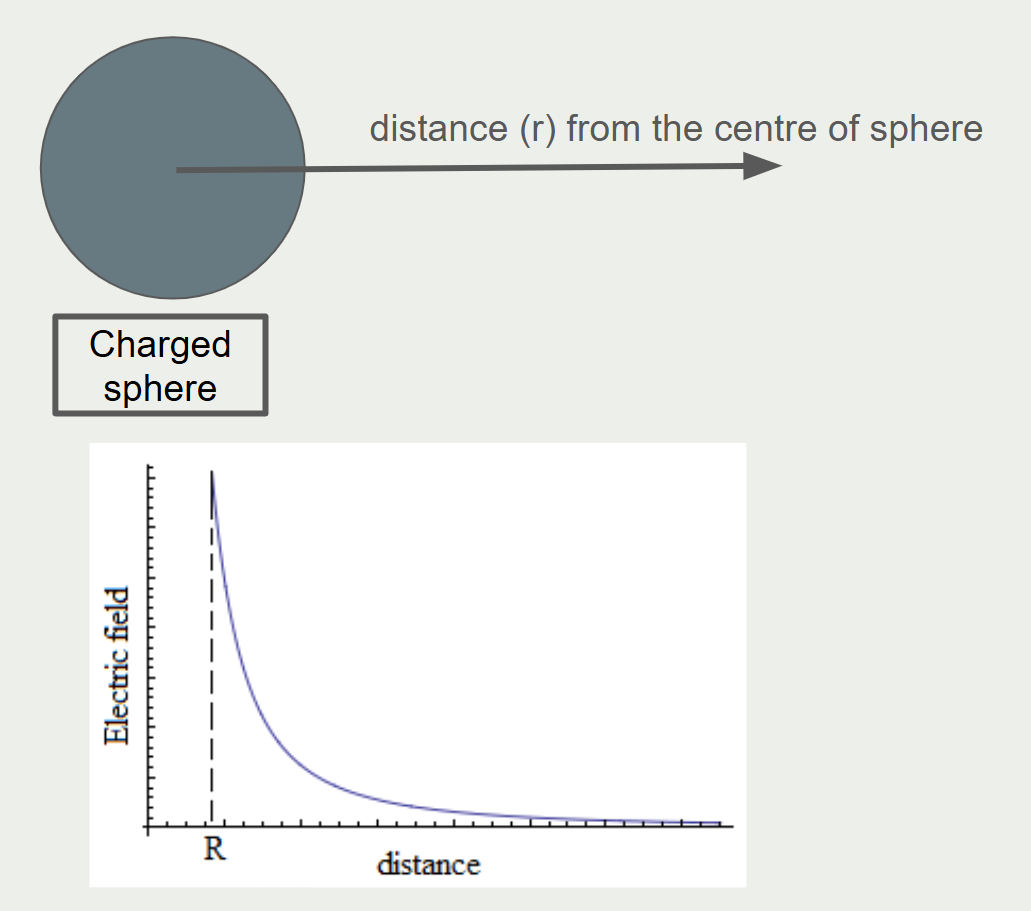
Electric field strength graph for one sphere

The electric field strength of a sphere is given by the equation $E = \frac{Q}{4 \pi \varepsilon_0 r^2}$.
Q represents the total charge on the sphere surface.
$𝜀_{0}$ is a constant that represents the permittivity of air.
E is zero inside the sphere as the charges are evenly spaced out on the surface of the sphere in a way that produces 0 field strength in the sphere.
E decreases as r increases outside the sphere as $𝜀_{0}$ and Q remain the same. Thus, $ E \propto \frac{1}{r^2} $

Electric field strength graph for two spheres

For two spheres, the electric field strength at a particular point is the sum of the field strengths of both spheres. In this case, it would be given by: $$E = \frac{Q_{A}}{4 \pi \varepsilon_0 r^2} \pm \frac{Q_{B}}{4 \pi \varepsilon_0 r^2}$$
A positive "test charge" is used. If the charge is pushed or pulled to the right, the force acting on the charge is positive. It does not matter if it is repelled or attracted.
If the charge is pushed or pulled to the left, the force acting on the charge is negative. It does not matter if it is repelled or attracted by a positive or negative sphere.
If the EFS always stays positive or negative, then the charges on both spheres are opposite. If the graph starts off as positive, the charge on sphere A is positive.
If the potential hits 0 and changes from positive to negative or negative to positive, it means that both of the spheres have the same charge. If it switches from positive to negative, sphere A is positively charged.